Ünlü Matematikçilere Kısa Bir Yolculuk

1.Thales

Antik Yunan döneminde yaşamış ve döneme damga vurmuş olan ünlü düşünür Thales ile yazıma başlamak istiyorum. Thales sadece matematik için değil felsefe için de çok önemli bir yerdedir çünkü felsefe tarihi Thales ile başlamıştır. İlk defa geometri için kendi mantıksal bir yapı geliştirdi ve ilk defa ispat düşüncesini geometriye Thales getirdi. Güneş tutulmasını, kendine özgü hesap yoluyla tahmin etmiş ve bu ona büyük bir saygınlık kazandırarak isminin duyulmasını sağlamıştır. Gölge boylarını inceleyerek nesnelerle olan orantısal ilişkileriyle piramitlerin boylarını hesaplamıştır.Thales’in yaptığı bazı ispatlar ise şunlardır.

-Çap daireyi 2 eş parçaya böler.

-İkizkenar üçgenin taban açıları eşittir.

-Yarım dairede çapı gören açı diktir.

-Benzer üçgenlerin kenarları oranlıdır.

-Benzer üçgenlerin kenarları oranlıdır. 

Bunun yanında Thales, geometrinin tümdengelimli  bir bilim olduğunu ortaya koymuştur.

2. Pisagor 

Bir anlatıya göre demirciler çalışırken örslerinden çıkan sesi duyan Pisagor ,bunun çok uyumlu olduğunu düşünmüş ve “Doğa kanunları buna izin veriyorsa bu kanunlar matematikseldir.” demiştir. Bundan hareketle, notaların matematiksel formüllere dönüştürülebileceğini keşfettiği söylenir. Sayılara bu denli değer veren Pisagor, sayılar üzerine Pisagor Okulunu kurmuştur.Onlar için her şey sayılara indirgenebilir. 

Pisagordan önce Moskova papirüslerinde 3-4-5 üçgeninin kullanımına, Mezopotamya tarihinde ise Pisagor teoremi uygulamalarına rastlanmıştır fakat bunu teorem haline getirememişlerdir daha sonradan Pisagor kendi adıyla anılan Pisagor teoreminin ispatını yapmıştır. 

3. Euclid (Öklid)

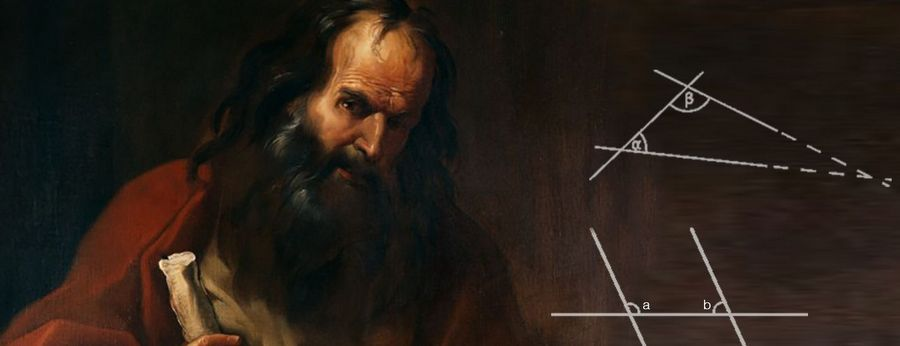
Antik Yunan zamanında yaşayan ve geometrinin babası olarak anılan en önemli matematikçilerden biridir. Yazdığı 13 ciltlik “Elementler” kitabı ile günümüz matematiğinin ve ismi ile anılan Öklid  Geometrisi’nin temelini atmıştır.  Elementler kitabında günümüz geometrisinin de temelini oluşturan 5 postulat bulunmaktadır. Bu 5 postulattan beşincisi matematik tarihinde önemli tartışmalara yol açarak Öklid dışı geometriler olarak adlandırılan yeni geometri alanlarının inşasına zemin hazırlamıştır.

Postulat: “Eğer bir doğru parçasını, iki doğrunun üzerinden geçecek şekilde çizerseniz ve aynı tarafta doksan dereceden daha az iki açı oluşursa, o zaman bu iki doğru kesişir.” ve Klasik dönemde Labochevsky ,Bolyai ve Riemann 5.postulatın yerine onun zıttı olan postulatlar ortaya koyarak iki yeni geometri oluşturulabileceğini göstermişlerdir. 

4. Labochevsky,

paralellik postulatını yok sayarak  hiperbolik geometriyi inşa etmiştir. Aynı zamanda birbirlerinden bağımsız olarak Bolyai de aynı sonuca ulaştığı için hiperbolik geometriye Labochevsky-Bolyai geometrisi denilmektedir. 

Riemann ise Riemann metriği ve eğriliği üzerinde tartışarak Riemann geometrisini (eliptik geometriyi) inşa etmiştir. 

Ne dersin ilerde farklı geometri alanları da ortaya çıkabilir mi?

İlayda İliman

17.01.2023