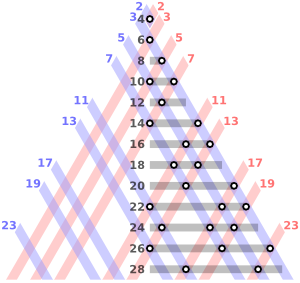
Goldbach Hipotezi: 280 Yıllık Bir Soru
Merhaba sevgili inekle Blog Okurları. Bugüne kadar hepimiz az veya çok matematik problemleriyle cebelleştik, kimisini çözdük kimisini ise yarıda bıraktık. Hatta bazen işin içinden dahi çıkamadık. Ara sıra komik cevaplar bulanlarımız da mutlaka vardır, mesela çocuğu babadan büyük bulmak gibi. En azından yanlış bir şeyler elde etmek bile hiçbir şey elde edememekten daha iyidir. Ancak bazı problemler vardır ki yanlış bir şeyler elde etmek, doğru bir şeyler elde etmekten daha avantajlı olabilir, en azından aslında öyle gibi görünenlerin öyle olmadığını anlatır. İşte tam burada 1742 yılında matematikçi Christian Goldbach tarafından ortaya atılan bir problemden bahsetmek istiyorum. Problem Christian Goldbach tarafından 18.yüzyılda şu ifadelerle ortaya konuldu: 2’den büyük her çift sayı iki asal sayının toplamı şeklinde yazılabilir.
Elbette ki bu, küçük sayılar için ispatı kolay olan bir problem. Örneğin: 8 = 5 + 3
28 = 5 + 23
84 = 41 + 43
Sayılar büyüdükçe zorluk seviyesi de doğal olarak artmakta. Örneğin: 126 = 59 + 67
162 = 79 + 83
186 = 97 + 89
Sayıları biraz daha büyütelim. Örneğin: 350 = 151 + 199
1302 = 619 + 683
1988 = 997 + 991
İşte bu şekilde yüzyıllar boyunca matematikçiler bu problemle uğraştılar. 1855 yılında Desboves, bu hipotezi 10.000’e kadar olan çift sayılarda doğruladı. Daha sonra 1940 yılında Pipping 100.000’e kadar olan çift sayılar için doğru olduğunu gösterdi. Daha sonra üst sınır 1964 yılında teknolojinin de yardımıyla, bilgisayar sayesinde 33.000.000’a, 1965’te 100.000.000’a; ve son olarak doğruluğu 1980’de 200.000.000’a kadar olan çift sayılarda ispatlandı. 1998 yılında ise Alman matematikçi Jörg Richstein, Goldbach’ın varsayımını 400 trilyona kadar olan tüm çift sayılarda doğruladı. 16 Şubat 2008’de Oliveira e Silva üst sınırı 1,1 kentilyon’a çıkardı! (yani, 1,1 kentilyon = 1.100.000.000.000.000.000). 2012 yılında ise bu üst sınır teknolojik gelişmeye paralel olarak, makineler yardımıyla 4 kentilyon’a kadar çıkarıldı ( yani, 4 kentilyon 4.000.000.000.000.000.000).
Üzerinden yaklaşık 280 yıl geçmesine rağmen günüzümde de Goldbach hipotezi doğru mu yanlış mı bilinmemekte. Buradaki temel sorunumuz aslında sonsuz sayıda asal sayının ve sonsuz sayıda tam sayının olmasında. Sanırım yanlış bir şeyler elde edilemezse bu problem sonsuza kadar çözülemeyecektir, çünkü sonlu olan bizler sonsuz olanlarla uğraşamayız. Eğer olur da problemin çözümüne yönelik doğru veya yanlış bir kanıtınız varsa tam olarak elde edeceğiniz ödül miktarı 1.000.000 dolar. Aksi halde bu problem matematiğin çözülememiş problemleri arasında yer almaya devam edecektir.
Emre Kahraman

14.09.2023